Woodwind

little by little

MLP和CNN SOC 加速器

发表于 更新于 分类于 Valine：
本文字数： 15k 阅读时长 ≈ 14 分钟
用SOC把MLP和CNN进行拆分成软硬件两部分，然后分别进行优化。硬件部分用FPGA对特定计算进行硬件加速，软件部分对特定代码配合硬件进行加速。

简介

用软硬件优先对频率高且能提升比例高的模块进行优化能获得更高的加速比。

1 找到频率高的模块

对kautodiff.h中的函数进行计数模拟，得出各个模块的使用频率。

2 对频率较高的模块进行分析，硬件是否能有较好的加速能力

最后选定了 kad_sdot, kad_saxpy-inlined和kad_vec_mul_sum等函数进行硬件加速。

函数特点

以下为mlp与CNN软件源码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
static inline float kad_sdot(int n, const float *x, const float *y) /* BLAS sdot */
{
    int i;
    float s = 0.;
    for (i = 0; i < n; ++i) s += x[i] * y[i];
    return s;
}
static inline void kad_saxpy_inlined(int n, float a, const float *x, float *y) // BLAS saxpy
{
    int i;
    for (i = 0; i < n; ++i) y[i] += a * x[i];
}
#endif

void kad_vec_mul_sum(int n, float *a, const float *b, const float *c)
{
    int i;
    for (i = 0; i < n; ++i) a[i] += b[i] * c[i];
}

根据以上代码，发现运用了大量的累加和乘法。根据硬件高并行的特点，浮点乘法可以有非常好的表现，浮点加法其次。

综上所述，开始编写浮点乘法和浮点加法的硬件。

硬件代码

浮点数


因为用的是IEEE-754标准的浮点数如图。标准为[1，8，23]，即一位符号位s，八位“指数”（e-127），二十三位小数m组成。


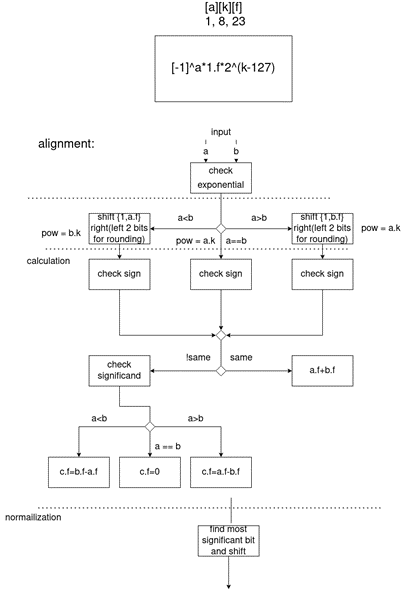
上图为Fadd 浮点数加法的大致结构图。

浮点数的运算浮点加法较为复杂，由三个主要部分组成。allignment, calculation和normalization。

1 allignment

在allignment阶段需要让两个加数处于同一个指数进行计算。所以需要比较两个加数的指数大小，小的加数需要右移指数差。同时m仅仅表示了小数部分，所以需要给两个数补一位最高位，同时赋值1。代码如下。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
module alignment(
input wire [7:0] k_a,
input wire [7:0] k_b,
output reg [7:0] pow_EX,
output reg [23:0] int_f_a,
output reg [23:0] int_f_b,
input wire [22:0] f_a,
input wire [22:0] f_b

);

//alignment: 
always @ (*) begin
	if (k_a > k_b) begin
		pow_EX = k_a;
		int_f_a = {1'b1,f_a};
		int_f_b = {1'b1,f_b} >> (k_a - k_b);
	end
	else if (k_b > k_a) begin
		pow_EX = k_b;
		int_f_a = {1'b1,f_a} >> (k_b - k_a);
		int_f_b = {1'b1,f_b};
	end
	else begin
		pow_EX = k_a;
		int_f_a = {1'b1,f_a};
		int_f_b = {1'b1,f_b};
	end		
end

endmodule
2 calculation

在计算阶段需要判断两个加数的符号，符号位相同较为容易，符号位不同需要判断哪个加数更大。加数大的符号位将成为合的符号位。代码如下。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
module calculation ( 
input wire s_a,
input wire s_b,
input wire [23:0] int_f_a,
input wire [23:0] int_f_b,
output reg [24:0] int_f_c
);


//calculation:
always @ (*) begin
	if (s_a == s_b) begin
		int_f_c = int_f_a + int_f_b;
	end
	else begin
		if (int_f_a < int_f_b) begin
			int_f_c = int_f_b - int_f_a;
		end
		else if (int_f_a > int_f_b) begin
			int_f_c = int_f_a - int_f_b;
		end
		else begin
			int_f_c = int_f_a - int_f_b;
		end 
	end		
end

endmodule
2 normalization

当两个加法运算结束时，需要考虑合是否符合IEEE-754标准。因为加法可能会有进位，减法可能会需要补位，即判断小数最高位再左移，同时指数相应减少。所以用了个蠢办法解决。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
module normailization (	
input wire s_a,
input wire s_b,
input wire [7:0] pow_EX,
input wire [24:0] int_f_c,
output reg [31:0] c
);


//normailization:
always @(*) begin
	case(int_f_c)

		25'b1xxxxxxxxxxxxxxxxxxxxxxxx: begin
			c[31] = (!s_a & s_b)|(s_a & !s_b);
			c[30:23] = pow_EX+8'd1;
			c[22:0] = int_f_c[23:1];
		end
		25'b1xxxxxxxxxxxxxxxxxxxxxxx: begin
			c[31] = (!s_a & s_b)|(s_a & !s_b);
			c[30:23] = pow_EX;
			c[22:0] = int_f_c[22:0];
		end	
	
		25'b1xxxxxxxxxxxxxxxxxxxxxx: begin
			c[31] = (!s_a & s_b)|(s_a & !s_b);
			c[30:23] = pow_EX-8'd1;
			c[22:0] = {int_f_c[21:0],1'b0};
		end	
		25'b1xxxxxxxxxxxxxxxxxxxxx: begin
			c[31] = (!s_a & s_b)|(s_a & !s_b);
			c[30:23] = pow_EX-8'd2;
			c[22:0] = {int_f_c[20:0],2'b0};
		end		

		25'b1xxxxxxxxxxxxxxxxxxxx: begin
			c[31] = (!s_a & s_b)|(s_a & !s_b);
			c[30:23] = pow_EX-8'd3;
			c[22:0] = {int_f_c[19:0],3'b0};
		end

		25'b1xxxxxxxxxxxxxxxxxxx: begin
			c[31] = (!s_a & s_b)|(s_a & !s_b);
			c[30:23] = pow_EX-8'd4;
			c[22:0] = {int_f_c[18:0],4'b0};
		end		
		25'b1xxxxxxxxxxxxxxxxxx: begin
			c[31] = (!s_a & s_b)|(s_a & !s_b);
			c[30:23] = pow_EX-8'd5;
			c[22:0] = {int_f_c[17:0],5'b0};
		end	
		25'b1xxxxxxxxxxxxxxxxx: begin
			c[31] = (!s_a & s_b)|(s_a & !s_b);
			c[30:23] = pow_EX-8'd6;
			c[22:0] = {int_f_c[16:0],6'b0};
		end	

		25'b1xxxxxxxxxxxxxxxx: begin
			c[31] = (!s_a & s_b)|(s_a & !s_b);
			c[30:23] = pow_EX-8'd7;
			c[22:0] = {int_f_c[15:0],7'b0};
		end
	
		25'b1xxxxxxxxxxxxxxx: begin
			c[31] = (!s_a & s_b)|(s_a & !s_b);
			c[30:23] = pow_EX-8'd8;
			c[22:0] = {int_f_c[14:0],8'b0};
		end		
		25'b1xxxxxxxxxxxxxx: begin
			c[31] = (!s_a & s_b)|(s_a & !s_b);
			c[30:23] = pow_EX-8'd9;
			c[22:0] = {int_f_c[13:0],9'b0};
		end	
		25'b1xxxxxxxxxxxxx: begin
			c[31] = (!s_a & s_b)|(s_a & !s_b);
			c[30:23] = pow_EX-8'd10;
			c[22:0] = {int_f_c[12:0],10'b0};
		end	

		25'b1xxxxxxxxxxxx: begin
			c[31] = (!s_a & s_b)|(s_a & !s_b);
			c[30:23] = pow_EX-8'd11;
			c[22:0] = {int_f_c[11:0],11'b0};
		end

		25'b1xxxxxxxxxxx: begin
			c[31] = (!s_a & s_b)|(s_a & !s_b);
			c[30:23] = pow_EX-8'd12;
			c[22:0] = {int_f_c[10:0],12'b0};
		end		
		25'b1xxxxxxxxxx: begin
			c[31] = (!s_a & s_b)|(s_a & !s_b);
			c[30:23] = pow_EX-8'd13;
			c[22:0] = {int_f_c[9:0],13'b0};
		end	
		25'b1xxxxxxxxx: begin
			c[31] = (!s_a & s_b)|(s_a & !s_b);
			c[30:23] = pow_EX-8'd14;
			c[22:0] = {int_f_c[8:0],14'b0};
		end	

		25'b1xxxxxxxx: begin
			c[31] = (!s_a & s_b)|(s_a & !s_b);
			c[30:23] = pow_EX-8'd15;
			c[22:0] = {int_f_c[7:0],15'b0};
		end
		25'b1xxxxxxx: begin
			c[31] = (!s_a & s_b)|(s_a & !s_b);
			c[30:23] = pow_EX-8'd16;
			c[22:0] = {int_f_c[6:0],16'b0};
		end	
		
		25'b1xxxxxx: begin
			c[31] = (!s_a & s_b)|(s_a & !s_b);
			c[30:23] = pow_EX-8'd17;
			c[22:0] = {int_f_c[5:0],17'b0};
		end	
		25'b1xxxxx: begin
			c[31] = (!s_a & s_b)|(s_a & !s_b);
			c[30:23] = pow_EX-8'd18;
			c[22:0] = {int_f_c[4:0],18'b0};
		end	
		25'b1xxxx: begin
			c[31] = (!s_a & s_b)|(s_a & !s_b);
			c[30:23] = pow_EX-8'd19;
			c[22:0] = {int_f_c[3:0],19'b0};
		end	
		25'b1xxx: begin
			c[31] = (!s_a & s_b)|(s_a & !s_b);
			c[30:23] = pow_EX-8'd20;
			c[22:0] = {int_f_c[2:0],20'b0};
		end	
		25'b1xx: begin
			c[31] = (!s_a & s_b)|(s_a & !s_b);
			c[30:23] = pow_EX-8'd21;
			c[22:0] = {int_f_c[1:0],21'b0};
		end	
		25'b1x: begin
			c[31] = (!s_a & s_b)|(s_a & !s_b);
			c[30:23] = pow_EX-8'd22;
			c[22:0] = {int_f_c[1],22'b0};
		end	
		25'b1: begin
			c[31] = (!s_a & s_b)|(s_a & !s_b);
			c[30:23] = pow_EX-8'd23;
			c[22:0] = 0;
		end	
		25'h0: begin
			c[31] = (!s_a & s_b)|(s_a & !s_b);
			c[30:23] = 0;
			c[22:0] = 0;
		end
	endcase
end
endmodule

测试结果

以上代码在验证时大部分通过，但是运行CNN时大量报错，结果发现在0时发现错误。然后发现存在对0的忽视。根据IEEE的定义：当数为0是指数e应该为0而不是任意数，所以加了特殊判断解决了0的问题。

但是偶尔还是有陆续的报错，随后发现精度上的问题。于是采用了最简单的四舍五入解决了这个问题，即加数最小再左边的一位。如果为1则进位，0则舍去。

但是最终出现了综合的问题，于是尽量合并always块防止多个always块时序上的问题，最终解决所有问题。最终硬件代码如下。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
module Fadd1(
//input wire clk,
//input wire reset,
//input wire clk_en,
//input wire start,
input wire [31:0] a,
input wire [31:0] b,
output wire [31:0] c
//output reg done
);
// {1:sign::s, 8:exponential::k-127, 23:significand::f}


//parameter idle = 2'b0;
//parameter processState = 2'b1;
//parameter doneState = 2'b10;
//reg done;
//reg [1:0]state, nstate;


reg [23:0] int_f_a, int_f_b;
reg [24:0] int_f_c;//1.f for a and b
reg [7:0] pow_EX;

wire [22:0] f_a, f_b;
wire [7:0] k_a, k_b;
reg int_s_c;
wire s_a, s_b;
reg [30:0] out;
//wire [31:0] out;
assign f_a = a[22:0];
assign f_b = b[22:0];
reg [6:0]case1;
assign k_a = a[30:23];
assign k_b = b[30:23];

assign s_a = a[31];
assign s_b = b[31];


//alignment: out[31]
always @ (*) begin
	if (k_a > k_b) begin
		int_s_c = s_a;
		pow_EX = k_a;
		int_f_a = {1'b1,f_a};
		int_f_b = {1'b1,f_b} >> (k_a - k_b);
		//calculation
		if (s_a == s_b) begin
			int_f_c = int_f_a + int_f_b;
		end
		else begin
			int_f_c = int_f_a - int_f_b;
		end	
	end
	else if (k_b > k_a) begin
		int_s_c = s_b;
		pow_EX = k_b;
		int_f_a = {1'b1,f_a} >> (k_b - k_a);
		int_f_b = {1'b1,f_b};
		//calculation
		if (s_a == s_b) begin
			int_f_c = int_f_a + int_f_b;
		end
		else begin
			int_f_c = int_f_b - int_f_a;
		end	
	end
	else begin
		
		pow_EX = k_a;
		int_f_a = {1'b1,f_a};
		int_f_b = {1'b1,f_b};
		//calculation
		if (s_a == s_b) begin
			int_f_c = int_f_a + int_f_b;
		end
		else begin
			if (int_f_a < int_f_b) begin
				int_s_c = s_b;
				int_f_c = int_f_b - int_f_a;
			end
			else if (int_f_a > int_f_b) begin
				int_s_c = s_a;
				int_f_c = int_f_a - int_f_b;
			end
			else begin
				int_s_c = 0;
				int_f_c = int_f_a - int_f_b;
			end 
		end	
	end		
end


always @(*) begin
	casex(int_f_c)

		25'b1xxxxxxxxxxxxxxxxxxxxxxxx: begin
			case1 = 7'd1;
			//out[31] = int_s_c;
			out[30:23] = pow_EX+8'd1;
			out[22:0] = int_f_c[23:1];
		end
		25'b1xxxxxxxxxxxxxxxxxxxxxxx: begin
			case1 = 7'd2;
			//out[31] = int_s_c;
			out[30:23] = pow_EX;
			out[22:0] = int_f_c[22:0];
		end	
	
		25'b1xxxxxxxxxxxxxxxxxxxxxx: begin
			case1 = 7'd3;
			//out[31] = (!s_a & s_b)|(s_a & !s_b);
			out[30:23] = pow_EX-8'd1;
			out[22:0] = {int_f_c[21:0],1'b0};
		end	
		25'b1xxxxxxxxxxxxxxxxxxxxx: begin
			case1 = 7'd4;
			//out[31] = (!s_a & s_b)|(s_a & !s_b);
			out[30:23] = pow_EX-8'd2;
			out[22:0] = {int_f_c[20:0],2'b0};
		end		

		25'b1xxxxxxxxxxxxxxxxxxxx: begin
			case1 = 7'd5;
			//out[31] = (!s_a & s_b)|(s_a & !s_b);
			out[30:23] = pow_EX-8'd3;
			out[22:0] = {int_f_c[19:0],3'b0};
		end

		25'b1xxxxxxxxxxxxxxxxxxx: begin
			case1 = 7'd6;
			//out[31] = (!s_a & s_b)|(s_a & !s_b);
			out[30:23] = pow_EX-8'd4;
			out[22:0] = {int_f_c[18:0],4'b0};
		end		
		25'b1xxxxxxxxxxxxxxxxxx: begin
			case1 = 7'd7;
			//out[31] = (!s_a & s_b)|(s_a & !s_b);
			out[30:23] = pow_EX-8'd5;
			out[22:0] = {int_f_c[17:0],5'b0};
		end	
		25'b1xxxxxxxxxxxxxxxxx: begin
			case1 = 7'd8;
			//out[31] = (!s_a & s_b)|(s_a & !s_b);
			out[30:23] = pow_EX-8'd6;
			out[22:0] = {int_f_c[16:0],6'b0};
		end	

		25'b1xxxxxxxxxxxxxxxx: begin
			case1 = 7'd9;
			//out[31] = (!s_a & s_b)|(s_a & !s_b);
			out[30:23] = pow_EX-8'd7;
			out[22:0] = {int_f_c[15:0],7'b0};
		end
	
		25'b1xxxxxxxxxxxxxxx: begin
			case1 = 7'd10;
			//out[31] = (!s_a & s_b)|(s_a & !s_b);
			out[30:23] = pow_EX-8'd8;
			out[22:0] = {int_f_c[14:0],8'b0};
		end		
		25'b1xxxxxxxxxxxxxx: begin
			case1 = 7'd11;
			//out[31] = (!s_a & s_b)|(s_a & !s_b);
			out[30:23] = pow_EX-8'd9;
			out[22:0] = {int_f_c[13:0],9'b0};
		end	
		25'b1xxxxxxxxxxxxx: begin
			case1 = 7'd12;
			//out[31] = (!s_a & s_b)|(s_a & !s_b);
			out[30:23] = pow_EX-8'd10;
			out[22:0] = {int_f_c[12:0],10'b0};
		end	

		25'b1xxxxxxxxxxxx: begin
			case1 = 7'd13;
			//out[31] = (!s_a & s_b)|(s_a & !s_b);
			out[30:23] = pow_EX-8'd11;
			out[22:0] = {int_f_c[11:0],11'b0};
		end

		25'b1xxxxxxxxxxx: begin
			case1 = 7'd14;
			//out[31] = (!s_a & s_b)|(s_a & !s_b);
			out[30:23] = pow_EX-8'd12;
			out[22:0] = {int_f_c[10:0],12'b0};
		end		
		25'b1xxxxxxxxxx: begin
			case1 = 7'd15;
			//out[31] = (!s_a & s_b)|(s_a & !s_b);
			out[30:23] = pow_EX-8'd13;
			out[22:0] = {int_f_c[9:0],13'b0};
		end	
		25'b1xxxxxxxxx: begin
			case1 = 7'd16;
			//out[31] = (!s_a & s_b)|(s_a & !s_b);
			out[30:23] = pow_EX-8'd14;
			out[22:0] = {int_f_c[8:0],14'b0};
		end	

		25'b1xxxxxxxx: begin
			case1 = 7'd17;
			//out[31] = (!s_a & s_b)|(s_a & !s_b);
			out[30:23] = pow_EX-8'd15;
			out[22:0] = {int_f_c[7:0],15'b0};
		end
		25'b1xxxxxxx: begin
			case1 = 7'd18;
			//out[31] = (!s_a & s_b)|(s_a & !s_b);
			out[30:23] = pow_EX-8'd16;
			out[22:0] = {int_f_c[6:0],16'b0};
		end	
		
		25'b1xxxxxx: begin
			case1 = 7'd19;
			//out[31] = (!s_a & s_b)|(s_a & !s_b);
			out[30:23] = pow_EX-8'd17;
			out[22:0] = {int_f_c[5:0],17'b0};
		end	
		25'b1xxxxx: begin
			case1 = 7'd20;
			//out[31] = (!s_a & s_b)|(s_a & !s_b);
			out[30:23] = pow_EX-8'd18;
			out[22:0] = {int_f_c[4:0],18'b0};
		end	
		25'b1xxxx: begin
			case1 = 7'd21;
			////out[31] = (!s_a & s_b)|(s_a & !s_b);
			out[30:23] = pow_EX-8'd19;
			out[22:0] = {int_f_c[3:0],19'b0};
		end	
		25'b1xxx: begin
			case1 = 7'd22;
			////out[31] = (!s_a & s_b)|(s_a & !s_b);
			out[30:23] = pow_EX-8'd20;
			out[22:0] = {int_f_c[2:0],20'b0};
		end	
		25'b1xx: begin
			case1 = 7'd23;
			////out[31] = (!s_a & s_b)|(s_a & !s_b);
			out[30:23] = pow_EX-8'd21;
			out[22:0] = {int_f_c[1:0],21'b0};
		end	
		25'b1x: begin
			case1 = 7'd24;
			////out[31] = (!s_a & s_b)|(s_a & !s_b);
			out[30:23] = pow_EX-8'd22;
			out[22:0] = {int_f_c[1],22'b0};
		end	
		25'b1: begin
			case1 = 7'd25;
			////out[31] = (!s_a & s_b)|(s_a & !s_b);
			out[30:23] = pow_EX-8'd23;
			out[22:0] = 0;
		end	
		25'h0: begin
			case1 = 7'd26;
			////out[31] = 0;
			out[30:23] = 0;
			out[22:0] = 0;
		end
	endcase
end
assign c = (out[22:0]!=23'b0)?{int_s_c,out[30:0]}:32'b0;
endmodule

经过测试硬件部分在NIOS II Custom instruction提速360%倍左右。至此硬件部分完成.

软件部分

其实软件部分需要优化的有很多，本人选择了最简单的一个办法：循环展开（loop unrolling）。因为FPGA是高并行的应用，所以需要极高的带宽，而cacheline的存在如果代码具有空间局部性（spatial locality），一次传输即可传输多个有用数据，cache 失效率（miss rate）会降低。观察如下代码。

1
2
3
4
5
6
7
static inline float kad_sdot(int n, const float *x, const float *y) /* BLAS sdot */
{
    int i;
    float s = 0.;
    for (i = 0; i < n; ++i) s += x[i] * y[i];
    return s;
}

每次读了x[i]下一次都会读y[i]然后读x[i+1]。所以冲突失效(conflict miss)会经常发生。如果改成如下代码，

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
static inline float kad_sdot(int n, const float *x, const float *y) /* BLAS sdot */
{
	int i;
		int n8 = n>>3<<3;
        int x8[8] = {0,0,0,0,0,0,0,0}
        int y8[8] = {0,0,0,0,0,0,0,0}
		float product,sum;
		float s = 0.;
		for (i = 0; i < n8; i+=8) {
            x8 = {x[i],x[i+1],x[i+2],x[i+3],x[i+4],x[i+5],x[i+6],x[i+7]};
            y8 = {y[i],y[i+1],y[i+2],y[i+3],y[i+4],y[i+5],y[i+6],y[i+7]};
			product =  ALT_CI_FMUL1_0(x8[0],y8[0]);
			//s += product;
			//sum = x[i]*y[i];
			s = ALT_CI_FADD1_0(s, product);
			product =  ALT_CI_FMUL1_0(x8[1],y8[1]);
			//s += product;
			//sum = x[i]*y[i];
			s = ALT_CI_FADD1_0(s, product);

			product =  ALT_CI_FMUL1_0(x8[2],y8[2]);
			//s += product;
			//sum = x[i]*y[i];
			s = ALT_CI_FADD1_0(s, product);
			product =  ALT_CI_FMUL1_0(x8[3],y8[3]);
			//s += product;
			//sum = x[i]*y[i];
			s = ALT_CI_FADD1_0(s, product);

			product =  ALT_CI_FMUL1_0(x8[4],y8[4]);
			//s += product;
			//sum = x[i]*y[i];
			s = ALT_CI_FADD1_0(s, product);
			product =  ALT_CI_FMUL1_0(x8[5],y8[5]);
			//s += product;
			//sum = x[i]*y[i];
			s = ALT_CI_FADD1_0(s, product);

			product =  ALT_CI_FMUL1_0(x8[6],y8[6]);
			//s += product;
			//sum = x[i]*y[i];
			s = ALT_CI_FADD1_0(s, product);
			product =  ALT_CI_FMUL1_0(x8[7],y8[7]);
			//s += product;
			//sum = x[i]*y[i];
			s = ALT_CI_FADD1_0(s, product);
		}
		for (; i < n; ++i) {
			product =  ALT_CI_FMUL1_0(x[i],y[i]);
			//s += product;
			//sum = x[i]*y[i];
			s = ALT_CI_FADD1_0(s, product);
		}
	return s;
}

取决于cacheline的大小，本人暂时假设cacheline能装下8个32位即8*4byte数据。

1
2
x8 = {x[i],x[i+1],x[i+2],x[i+3],x[i+4],x[i+5],x[i+6],x[i+7]};
y8 = {y[i],y[i+1],y[i+2],y[i+3],y[i+4],y[i+5],y[i+6],y[i+7]};

上述代码可以增加吞吐量。

同时运算为乘加，所以s会加上乘法算出来的积。因为NIOS II采用了流水线，同时具有并行处理的功能。如果浮点数乘法不能在一个时钟周期结束，就会让流水线停滞。所以循环展开后，可以改为如下代码解决数据依赖导致（data dependency）的流水线停滞。

1
2
3
4
5
6
7
8
9
product =  ALT_CI_FMUL1_0(x8[0],y8[0]);  
product1 =  ALT_CI_FMUL1_0(x8[1],y8[1]);  
product2 =  ALT_CI_FMUL1_0(x8[2],y8[2]);
product3 =  ALT_CI_FMUL1_0(x8[3],y8[3]);

s = ALT_CI_FADD1_0(s, product);
s = ALT_CI_FADD1_0(s, product1);
s = ALT_CI_FADD1_0(s, product2);
s = ALT_CI_FADD1_0(s, product3);

当然上述代码改进默认采用的是非乱序的处理器。
至此软件优化结束。

总性能提升

number of images 1 5 10 100
CNN-Original 26.65495 135.10212 270.72152 2715.26287
CNN-CI 4.83646 24.185 48.37042 483.76189
Speedup (Times) 5.51125x 5.58619x 5.59684x 5.61280x

最终在加上软件的优化后，总性能提升562%左右